Margin Methods#

Suppose that \(\mathbf{P}\) is a profile. We write \(\mathcal{M}(\mathbf{P})\) for the margin graph of \(\mathbf{P}\).

A voting method \(F\) is margin-based if it satisfies the following invariance property: For all \(\mathbf{P}, \mathbf{P}'\), if \(\mathcal{M}(\mathbf{P})= \mathcal{M}(\mathbf{P}')\), then \(F(\mathbf{P}) = F(\mathbf{P}')\).

Minimax#

pref_voting.margin_based_methods.minimax(edata, curr_cands=None, strength_function=None)[source]#

The Minimax winners are the candidates with the smallest maximum pairwise loss. That is, for each candidate \(a\), find the biggest margin of a candidate \(b\) over \(a\), then elect the candidate(s) with the smallest such loss. Also known as the Simpson-Kramer Rule.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
    
prof = Profile([[3, 0, 1, 2], [1, 3, 2, 0], [1, 3, 0, 2], [1, 2, 0, 3], [3, 2, 0, 1], [0, 2, 1, 3]], [1, 1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)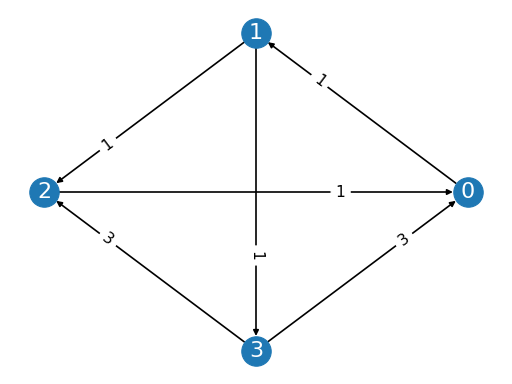

from pref_voting.margin_based_methods import minimax

minimax.display(prof)

Minimax winners are {1, 3}

Minimax Scores#

pref_voting.margin_based_methods.minimax_scores(edata, curr_cands=None, score_method='margins')[source]#

Return the minimax scores for each candidate, where the minimax score for \(c\) is -1 * the maximum pairwise majority loss.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
score_method (str, optional) – Options include “margins” (the default), “winning” assigns to each candidate \(c\) the maximum support of a candidate majority preferred to \(c\), and “pairwise_opposition” assigns to each candidate \(c\) the maximum support of any candidate over \(c\). These scores only lead to different results on non-linear profiles.

Returns:

A dictionary associating each candidate with its minimax score.

Example:

from pref_voting.profiles import Profile
    
prof = Profile([[3, 0, 1, 2], [1, 3, 2, 0], [1, 3, 0, 2], [1, 2, 0, 3], [3, 2, 0, 1], [0, 2, 1, 3]], [1, 1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.margin_based_methods import minimax_scores, minimax

minimax.display(prof)
print(minimax_scores(prof))

Minimax winners are {1, 3}
{0: -3, 1: -1, 2: -3, 3: -1}

Beat Path#

pref_voting.margin_based_methods.beat_path(edata, curr_cands=None, strength_function=None)[source]#

For candidates \(a\) and \(b\), a path from \(a\) to \(b\) is a sequence \(x_1, \ldots, x_n\) of distinct candidates with \(x_1=a\) and \(x_n=b\) such that for \(1\leq k\leq n-1\), \(x_k\) is majority preferred to \(x_{k+1}\). The strength of a path is the minimal margin along that path. Say that \(a\) defeats \(b\) according to Beat Path if the the strength of the strongest path from \(a\) to \(b\) is greater than the strength of the strongest path from \(b\) to \(a\). Then, the candidates that are undefeated according to Beat Path are the winners. Also known as the Schulze Rule.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)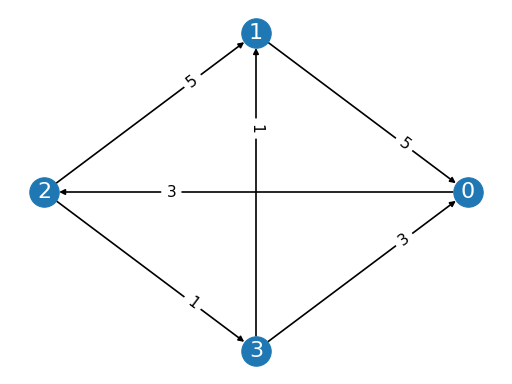

from pref_voting.margin_based_methods import beat_path

beat_path.display(mg)

Beat Path winner is {3}

Beat Path Floyd-Warshall#

pref_voting.margin_based_methods.beat_path_Floyd_Warshall(edata, curr_cands=None, strength_function=None)[source]#

An implementation of Beat Path using a variation of the Floyd-Warshall Algorithm See https://en.wikipedia.org/wiki/Schulze_method#Implementation)

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)

from pref_voting.margin_based_methods import beat_path_Floyd_Warshall

beat_path.display(mg)
beat_path_Floyd_Warshall.display(mg)

Beat Path winner is {3}
Beat Path winner is {3}

Beat Path Defeat#

pref_voting.margin_based_methods.beat_path_defeat(edata, curr_cands=None, strength_function=None)[source]#

Returns the defeat relation for Beat Path.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A networkx DiGraph representing the Beat Path defeat relation.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import beat_path_defeat

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display_with_defeat(beat_path_defeat(mg))

(Source code, png, pdf)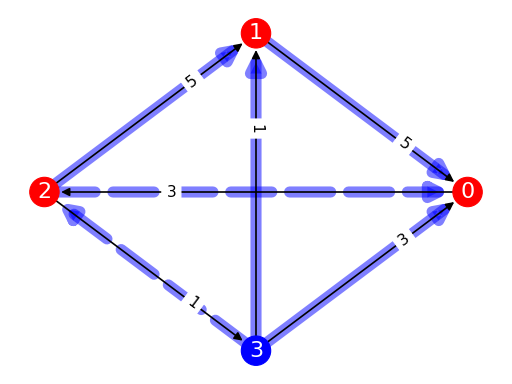

Split Cycle#

pref_voting.margin_based_methods.split_cycle(edata, curr_cands=None, strength_function=None)[source]#

A majority cycle is a sequence \(x_1, \ldots ,x_n\) of distinct candidates with \(x_1=x_n\) such that for \(1 \leq k \leq n-1\), \(x_k\) is majority preferred to \(x_{k+1}\). The Split Cycle winners are determined as follows:

If candidate x has a positive margin over y and (x,y) is not the weakest edge in a cycle, then x defeats y. Equivalently, if x has a positive margin over y and there is no path from y back to x of strength at least the margin of x over y, then x defeats y.

The candidates that are undefeated are the Split Cycle winners.

See https://github.com/epacuit/splitcycle and the paper https://arxiv.org/abs/2004.02350 for more information.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)

from pref_voting.margin_based_methods import split_cycle

split_cycle.display(mg)

Split Cycle winners are {2, 3}

Split Cycle Floyd-Warshall#

pref_voting.margin_based_methods.split_cycle_Floyd_Warshall(edata, curr_cands=None, strength_function=None)[source]#

An implementation of Split Cycle based on the Floyd-Warshall Algorithm.

See https://github.com/epacuit/splitcycle and the paper https://arxiv.org/abs/2004.02350 for more information.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)

from pref_voting.margin_based_methods import split_cycle, split_cycle_Floyd_Warshall

split_cycle.display(mg)
split_cycle_Floyd_Warshall.display(mg)

Split Cycle winners are {2, 3}
Split Cycle winners are {2, 3}

Split Cycle Defeat#

pref_voting.margin_based_methods.split_cycle_defeat(edata, curr_cands=None, strength_function=None)[source]#

Returns the Split Cycle defeat relation.

See https://arxiv.org/abs/2008.08451 for an extended discussion of this notion of defeat in an election.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A networkx DiGraph representing the Split Cycle defeat relation.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import split_cycle_defeat

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display_with_defeat(split_cycle_defeat(mg))

(Source code, png, pdf)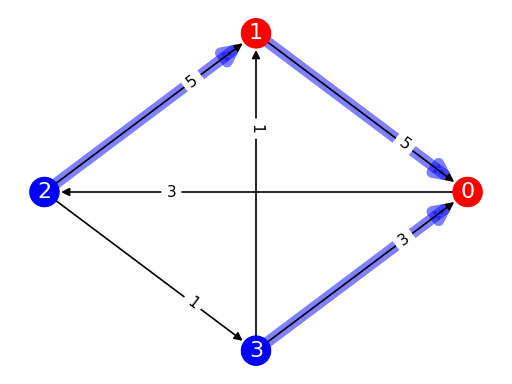

Ranked Pairs#

pref_voting.margin_based_methods.ranked_pairs(edata, curr_cands=None, strength_function=None)[source]#

Order the edges in the margin graph from largest to smallest and lock them in in that order, skipping edges that create a cycle. If there are ties in the margins, break the ties using a tie-breaking rule: a linear ordering over the edges. A candidate is a Ranked Pairs winner if it wins according to some tie-breaking rule. Also known as Tideman’s Rule.

Warning

This method can take a very long time to find winners.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)

from pref_voting.margin_based_methods import ranked_pairs

ranked_pairs.display(mg)

Ranked Pairs winner is {2}

Ranked Pairs with Test#

pref_voting.margin_based_methods.ranked_pairs_with_test(edata, curr_cands=None, strength_function=None)[source]#

Find the Ranked Pairs winners, but include a test to determined if it will take too long to compute the Ranked Pairs winners. If the calculation of the winners will take too long, return None.

Important

This voting method that might return None rather than a list of candidates.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(1, 2, 2), (1, 3, 2), (2, 0, 2)])

mg.display()

(Source code, png, pdf)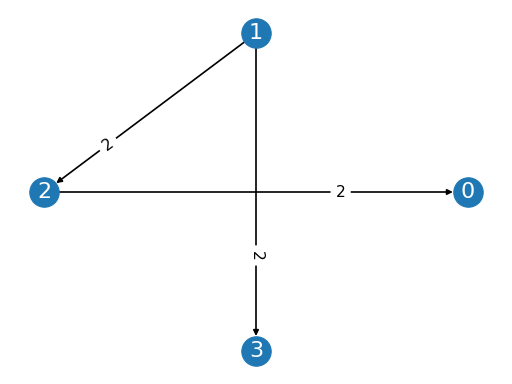

from pref_voting.margin_based_methods import ranked_pairs_with_test

ranked_pairs_with_test.display(mg)

Ranked Pairs winning set is not available

Ranked Pairs Defeats#

pref_voting.margin_based_methods.ranked_pairs_defeats(edata, curr_cands=None, strength_function=None)[source]#

Returns the Ranked Pairs defeat relations produced by the Ranked Pairs algorithm.

Important

Unlike the other functions that return a single defeat relation, this returns a list of defeat relations.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A networkx DiGraph representing the Ranked Pairs defeat relation.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 1, 10), (0, 2, 2), (1, 3, 4), (2, 1, 6), (2, 3, 8), (3, 0, 4)])

mg.display()

(Source code, png, pdf)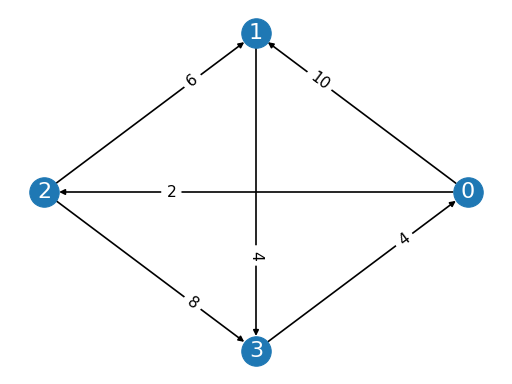

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import ranked_pairs_defeats

mg = MarginGraph([0, 1, 2, 3], [(0, 1, 10), (0, 2, 2), (1, 3, 4), (2, 1, 6), (2, 3, 8), (3, 0, 4)])
rp_defeats = ranked_pairs_defeats(mg)

for rpd in rp_defeats:
    print(rpd.edges)

[(0, 1), (0, 2), (1, 3), (2, 3), (2, 1)]
[(0, 1), (2, 3), (2, 1), (3, 0)]

Ranked Pairs from Stacks#

pref_voting.margin_based_methods.is_stack(edata, cand_list, curr_cands=None)[source]#

A stack is a linear order \(L\) on the candidate such that for all candidates \(a\) and \(b\), if \(aLb\), then there are distinct candidates \(x_1,\dots,x_n\) with \(x_1=a\) and \(x_n=b\) such that \(x_i L x_{i+1}\) and for all \(i\in \{1,\dots, n-1\}\), the margin of \(x_1\) over \(x_{i+1}\) is greater than or equal to the margin of \(b\) over \(a\).

This definition is due to Zavist and Tideman 1989, and is used as an alternative characterization of Ranked Pairs: \(a\) is a Ranked Pairs winner if and only if \(a\) is the maximum element of some stack.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
cand_list (list) – The list of candidates that may be a stack
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

True if cand_list is a stack and False otherwise

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2], [(0, 1, 2), (1, 2, 4), (2, 0, 2)])

mg.display()

(Source code, png, pdf)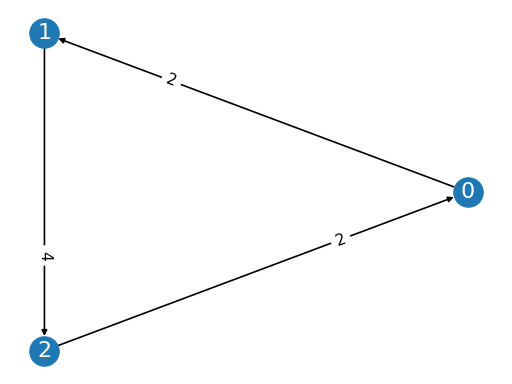

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import is_stack
from itertools import permutations

mg = MarginGraph([0, 1, 2], [(0, 1, 2), (1, 2, 4), (2, 0, 2)])

for clist in permutations(mg.candidates):
    print(f"{clist} {'is' if is_stack(mg, clist) else 'is not'} a stack")

(0, 1, 2) is a stack
(0, 2, 1) is not a stack
(1, 0, 2) is not a stack
(1, 2, 0) is a stack
(2, 0, 1) is not a stack
(2, 1, 0) is not a stack

pref_voting.margin_based_methods.ranked_pairs_from_stacks(edata, curr_cands=None)[source]#

Find the Ranked Pairs winners by iterating over all permutations of candidates (restricted to curr_cands if not None), and checking if the list is a stack.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 3), (1, 0, 5), (2, 1, 5), (2, 3, 1), (3, 0, 3), (3, 1, 1)])

mg.display()

(Source code, png, pdf)

from pref_voting.margin_based_methods import ranked_pairs, ranked_pairs_from_stacks

ranked_pairs.display(mg)
ranked_pairs_from_stacks.display(mg)

Ranked Pairs winner is {2}
Ranked Pairs winner is {2}

Ranked Pairs with Tiebreaking#

pref_voting.margin_based_methods.ranked_pairs_tb(edata, curr_cands=None, tie_breaker=None, strength_function=None)[source]#

Ranked Pairs with a fixed linear order on the candidates to break any ties in the margins. Since the tie_breaker is a linear order, this method is resolute.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

from pref_voting.profiles import Profile
from pref_voting.margin_based_methods import ranked_pairs_from_stacks, ranked_pairs_tb, ranked_pairs_zt

prof = Profile([[2, 3, 1, 0], [0, 3, 1, 2], [1, 3, 2, 0], [2, 1, 3, 0]], [1, 1, 1, 1])

prof.display()

ranked_pairs_from_stacks.display(prof)
ranked_pairs_tb.display(prof)
ranked_pairs_tb.display(prof, tie_breaker = [3, 2, 1, 0])
ranked_pairs_zt.display(prof)

+---+---+---+---+
| 1 | 1 | 1 | 1 |
+---+---+---+---+
| 2 | 0 | 1 | 2 |
| 3 | 3 | 3 | 1 |
| 1 | 1 | 2 | 3 |
| 0 | 2 | 0 | 0 |
+---+---+---+---+
Ranked Pairs winners are {1, 2, 3}
Ranked Pairs TB winner is {1}
Ranked Pairs TB winner is {3}
Ranked Pairs ZT winner is {2}

pref_voting.margin_based_methods.ranked_pairs_zt(profile, curr_cands=None, strength_function=None)[source]#

Ranked pairs where a fixed voter breaks any ties in the margins. It is always the voter in position 0 that breaks the ties. Since voters have strict preferences, this method is resolute. This is known as Ranked Pairs ZT, for Zavist Tideman.

Parameters:

edata (Profile) – A profile of linear orders
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates.

from pref_voting.profiles import Profile
from pref_voting.margin_based_methods import ranked_pairs_from_stacks, ranked_pairs_tb, ranked_pairs_zt

prof = Profile([[2, 3, 1, 0], [0, 3, 1, 2], [1, 3, 2, 0], [2, 1, 3, 0]], [1, 1, 1, 1])

prof.display()

ranked_pairs_from_stacks.display(prof)
ranked_pairs_tb.display(prof)
ranked_pairs_tb.display(prof, tie_breaker = [3, 2, 1, 0])
ranked_pairs_zt.display(prof)

+---+---+---+---+
| 1 | 1 | 1 | 1 |
+---+---+---+---+
| 2 | 0 | 1 | 2 |
| 3 | 3 | 3 | 1 |
| 1 | 1 | 2 | 3 |
| 0 | 2 | 0 | 0 |
+---+---+---+---+
Ranked Pairs winners are {1, 2, 3}
Ranked Pairs TB winner is {1}
Ranked Pairs TB winner is {3}
Ranked Pairs ZT winner is {2}

River#

pref_voting.margin_based_methods.river(edata, curr_cands=None, strength_function=None)[source]#

Order the edges in the weak margin graph from largest to smallest and lock them in in that order, skipping edges that create a cycle and edges in which there is already an edge pointing to the target. Break ties using a tie-breaking linear ordering over the edges. A candidate is a River winner if it wins according to some tie-breaking rule. See https://electowiki.org/wiki/River.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import river, ranked_pairs

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 2), (0, 3, 8), (1, 0, 12), (2, 3, 12), (3, 1, 6)])

ranked_pairs.display(mg)
river.display(mg)

Ranked Pairs winner is {1}
River winner is {2}

pref_voting.margin_based_methods.river_with_test(edata, curr_cands=None, strength_function=None)[source]#

Find the River winners with a test to determined if it will take too long to compute the River winners. If the calculation of the winners will take too long, return None.

Important

This voting method that might return None rather than a list of candidates.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

River with Tiebreaking#

pref_voting.margin_based_methods.river_tb(edata, curr_cands=None, tie_breaker=None, strength_function=None)[source]#

River with a fixed linear order on the candidates to break any ties in the margins. Since the tie_breaker is a linear order, this method is resolute.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
tie_breaker (List[int], optional) – A linear order on the candidates. If not set, then the candidates are sorted in ascending order.
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

pref_voting.margin_based_methods.river_zt(profile, curr_cands=None, strength_function=None)[source]#

River where a fixed voter breaks any ties in the margins. It is always the voter in position 0 that breaks the ties. Since voters have strict preferences, this method is resolute.

Parameters:

edata (Profile) – A profile of linear orders
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates.

Stable Voting#

pref_voting.margin_based_methods.stable_voting(edata, curr_cands=None, strength_function=None)[source]#

Implementation of Stable Voting from https://arxiv.org/abs/2108.00542.

Stable Voting is a recursive voting method defined as follows:

If there is only one candidate in the profile, then that candidate is the winner.
Order the pairs \((a,b)\) of candidates from largest to smallest value of the margin of \(a\) over \(b\) such that \(a\) is undefeated according to Split Cycle, and declare as Stable Voting winners the candidate(s) \(a\) from the earliest pair(s) \((a,b)\) such that \(a\) is a Simple Stable Voting winner in the election without \(b\).

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

See also

pref_voting.margin_based_methods.simple_stable_faster(), pref_voting.margin_based_methods.simple_stable_voting()

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import stable_voting

mg = MarginGraph([0, 1, 2, 3], [(0, 3, 8), (1, 0, 10), (2, 0, 4), (2, 1, 8), (3, 1, 8)])

stable_voting.display(mg)

Stable Voting winner is {2}

Stable Voting Faster#

pref_voting.margin_based_methods.stable_voting_faster(edata, curr_cands=None, strength_function=None)[source]#

Stable Voting is Condorcet consistent. It is faster to skip executing the recursive algorithm when there is a Condorcet winner.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import stable_voting, stable_voting_faster

mg = MarginGraph([0, 1, 2, 3], [(0, 3, 8), (1, 0, 10), (2, 0, 4), (2, 1, 8), (3, 1, 8)])

stable_voting_faster.display(mg)
stable_voting.display(mg)

Stable Voting winner is {2}
Stable Voting winner is {2}

Simple Stable Voting#

pref_voting.margin_based_methods.simple_stable_voting(edata, curr_cands=None, strength_function=None)[source]#

Implementation of Simple Stable Voting from https://arxiv.org/abs/2108.00542.

Simple Stable Voting is a recursive voting method defined as follows:

If there is only one candidate in the profile, then that candidate is the winner.
Order the pairs \((a,b)\) of candidates from largest to smallest value of the margin of \(a\) over \(b\), and declare as Simple Stable Voting winners the candidate(s) \(a\) from the earliest pair(s) \((a,b)\) such that \(a\) is a Simple Stable Voting winner in the election without \(b\).

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import simple_stable_voting

mg = MarginGraph([0, 1, 2, 3], [(0, 3, 8), (1, 0, 10), (2, 0, 4), (2, 1, 8), (3, 1, 8)])

simple_stable_voting.display(mg)

Simple Stable Voting winner is {2}

Simple Stable Voting Faster#

pref_voting.margin_based_methods.simple_stable_voting_faster(edata, curr_cands=None, strength_function=None)[source]#

Simple Stable Voting is Condorcet consistent. It is faster to skip executing the recursive algorithm when there is a Condorcet winnerFirst check if there is a Condorcet winner. If so, return the Condorcet winner, otherwise find the Simple Stable Voting winner using _simple_stable_voting

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands
strength_function (function, optional) – The strength function to be used to calculate the strength of a path. The default is the margin method of edata. This only matters when the ballots are not linear orders.

Returns:

A sorted list of candidates.

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.margin_based_methods import simple_stable_voting, simple_stable_voting_faster

mg = MarginGraph([0, 1, 2, 3], [(0, 3, 8), (1, 0, 10), (2, 0, 4), (2, 1, 8), (3, 1, 8)])

simple_stable_voting_faster.display(mg)
simple_stable_voting.display(mg)

Simple Stable Voting winner is {2}
Simple Stable Voting winner is {2}

Loss-Trimmer#

pref_voting.margin_based_methods.loss_trimmer(edata, curr_cands=None)[source]#

Iteratively eliminate the candidate with the largest sum of margins of loss until a Condorcet winner is found. In this version of the method, parallel-universe tiebreaking is used if there are multiple candidates with the largest sum of margins of loss.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Note

Method proposed by Richard B. Darlington in “The Case for the Loss-Trimmer Voting System.”