(Weighted) Majority Graphs¶

A majority graph is a directed asymmetric graph in which the nodes are the candidates and an edge from \(a\) to \(b\) means that \(a\) is majority preferred to \(b\).

A MajorityGraph has a number of methods used by voting methods.

from pref_voting.weighted_majority_graphs import MajorityGraph

mg = MajorityGraph([0, 1, 2], [(0, 1), (1, 2), (2, 0)])

print(mg.edges)
for c1 in mg.candidates:
    for c2 in mg.candidates:
        print(f"{c1} is majority preferred to {c2}: {mg.majority_prefers(c1, c2)}")
        print(f"{c1} is tied with {c2}: {mg.is_tied(c1, c2)}")

for c in mg.candidates:
    print(f"The dominators of {c} are {mg.dominators(c)}")
    print(f"The candidates that {c} dominates are {mg.dominates(c)}")

print(f"Copeland scores: {mg.copeland_scores()}")
print(f"Condorcet winner: {mg.condorcet_winner()}")
print(f"Weak Condorcet winners: {mg.weak_condorcet_winner()}")
print(f"Condorcet loser: {mg.condorcet_loser()}")

print()

mg2 = MajorityGraph([0, 1, 2], [(0, 1), (1, 2)])

print(mg2.edges)
for c1 in mg2.candidates:
    for c2 in mg2.candidates:
        print(f"{c1} is majority preferred to {c2}: {mg2.majority_prefers(c1, c2)}")
        print(f"{c1} is tied with {c2}: {mg2.is_tied(c1, c2)}")

for c in mg2.candidates:
    print(f"The dominators of {c} are {mg2.dominators(c)}")
    print(f"The candidates that {c} dominates are {mg2.dominates(c)}")

print(f"Copeland scores: {mg2.copeland_scores()}")
print(f"Condorcet winner: {mg2.condorcet_winner()}")
print(f"Weak Condorcet winners: {mg2.weak_condorcet_winner()}")
print(f"Condorcet loser: {mg2.condorcet_loser()}")

[(0, 1), (1, 2), (2, 0)]
0 is majority preferred to 0: False
0 is tied with 0: True
0 is majority preferred to 1: True
0 is tied with 1: False
0 is majority preferred to 2: False
0 is tied with 2: False
1 is majority preferred to 0: False
1 is tied with 0: False
1 is majority preferred to 1: False
1 is tied with 1: True
1 is majority preferred to 2: True
1 is tied with 2: False
2 is majority preferred to 0: True
2 is tied with 0: False
2 is majority preferred to 1: False
2 is tied with 1: False
2 is majority preferred to 2: False
2 is tied with 2: True
The dominators of 0 are [2]
The candidates that 0 dominates are [1]
The dominators of 1 are [0]
The candidates that 1 dominates are [2]
The dominators of 2 are [1]
The candidates that 2 dominates are [0]
Copeland scores: {0: 0.0, 1: 0.0, 2: 0.0}
Condorcet winner: None
Weak Condorcet winners: None
Condorcet loser: None

[(0, 1), (1, 2)]
0 is majority preferred to 0: False
0 is tied with 0: True
0 is majority preferred to 1: True
0 is tied with 1: False
0 is majority preferred to 2: False
0 is tied with 2: True
1 is majority preferred to 0: False
1 is tied with 0: False
1 is majority preferred to 1: False
1 is tied with 1: True
1 is majority preferred to 2: True
1 is tied with 2: False
2 is majority preferred to 0: False
2 is tied with 0: True
2 is majority preferred to 1: False
2 is tied with 1: False
2 is majority preferred to 2: False
2 is tied with 2: True
The dominators of 0 are []
The candidates that 0 dominates are [1]
The dominators of 1 are [0]
The candidates that 1 dominates are [2]
The dominators of 2 are [1]
The candidates that 2 dominates are []
Copeland scores: {0: 1.0, 1: 0.0, 2: -1.0}
Condorcet winner: None
Weak Condorcet winners: [0]
Condorcet loser: None

A margin graph is a weighted directed asymmetric graph in which the nodes are the candidates, an edge from \(a\) to \(b\) means that \(a\) is majority preferred to \(b\), and the weight of the edge is the margin of \(a\) over \(b\).

A MarginGraph has a number of methods used by voting methods.

Important

The weights of a MarginGraph can be any numbers. However, if the weights are generated by a profile of linear orders, then the weights will have the same parity (which is even if there is any zero margin between distinct candidates).

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2], [(0, 1, 1), (1, 2, 3), (2, 0, 3)])

print(mg.edges)
for c1 in mg.candidates:
    for c2 in mg.candidates:
        print(f"the margin of {c1} over {c2} is {mg.margin(c1, c2)}")
        print(f"{c1} is majority preferred to {c2}: {mg.majority_prefers(c1, c2)}")
        print(f"{c1} is tied with {c2}: {mg.is_tied(c1, c2)}")

for c in mg.candidates:
    print(f"The dominators of {c} are {mg.dominators(c)}")
    print(f"The candidates that {c} dominates are {mg.dominates(c)}")

print(f"Copeland scores: {mg.copeland_scores()}")
print(f"Condorcet winner: {mg.condorcet_winner()}")
print(f"Weak Condorcet winners: {mg.weak_condorcet_winner()}")
print(f"Condorcet loser: {mg.condorcet_loser()}")

[(0, 1, 1), (1, 2, 3), (2, 0, 3)]
the margin of 0 over 0 is 0
0 is majority preferred to 0: False
0 is tied with 0: True
the margin of 0 over 1 is 1
0 is majority preferred to 1: True
0 is tied with 1: False
the margin of 0 over 2 is -3
0 is majority preferred to 2: False
0 is tied with 2: False
the margin of 1 over 0 is -1
1 is majority preferred to 0: False
1 is tied with 0: False
the margin of 1 over 1 is 0
1 is majority preferred to 1: False
1 is tied with 1: True
the margin of 1 over 2 is 3
1 is majority preferred to 2: True
1 is tied with 2: False
the margin of 2 over 0 is 3
2 is majority preferred to 0: True
2 is tied with 0: False
the margin of 2 over 1 is -3
2 is majority preferred to 1: False
2 is tied with 1: False
the margin of 2 over 2 is 0
2 is majority preferred to 2: False
2 is tied with 2: True
The dominators of 0 are [2]
The candidates that 0 dominates are [1]
The dominators of 1 are [0]
The candidates that 1 dominates are [2]
The dominators of 2 are [1]
The candidates that 2 dominates are [0]
Copeland scores: {0: 0.0, 1: 0.0, 2: 0.0}
Condorcet winner: None
Weak Condorcet winners: None
Condorcet loser: None

Both :class:~pref_voting.weighted_majority_graphs.MarginGraph` and :class:~pref_voting.weighted_majority_graphs.MajorityGraph` can be generated from a profile.

from pref_voting.profiles import Profile
from pref_voting.profiles_with_ties import ProfileWithTies

prof = Profile([[0, 1, 2], [2, 0, 1], [1, 0, 2]], rcounts=[2, 1, 2])

prof.display()

majg = prof.majority_graph()
print(f"The majority graph edges are {majg.edges}")

mg = prof.margin_graph()
print(f"The margin graph edges are {mg.edges}")

prof2 = ProfileWithTies([{0: 1, 1: 2, 2: 3}, {1:1, 2:1, 0:2}, {2:1, 0:2}], [2, 3, 1])
prof2.display()

majg = prof2.majority_graph()
print(f"The majority graph edges are {majg.edges}")

mg = prof2.margin_graph()
print(f"The margin graph edges are {mg.edges}")

+---+---+---+
| 2 | 1 | 2 |
+---+---+---+
| 0 | 2 | 1 |
| 1 | 0 | 0 |
| 2 | 1 | 2 |
+---+---+---+
The majority graph edges are [(0, 1), (0, 2), (1, 2)]
The margin graph edges are [(0, 1, 1), (0, 2, 3), (1, 2, 3)]
+---+-----+---+
| 2 |  3  | 1 |
+---+-----+---+
| 0 | 1 2 | 2 |
| 1 |  0  | 0 |
| 2 |     |   |
+---+-----+---+
The majority graph edges are [(1, 0), (1, 2), (2, 0)]
The margin graph edges are [(1, 0, 1), (1, 2, 2), (2, 0, 2)]

MajorityGraph Class¶

class pref_voting.weighted_majority_graphs.MajorityGraph(candidates, edges, cmap=None)[source]¶

A majority graph is an asymmetric directed graph. The nodes are the candidates and an edge from candidate \(c\) to \(d\) means that \(c\) is majority preferred to \(d\).

Parameters:

candidates (list[int] or list[str]) – List of the candidates. To be used as nodes in the majority graph.
edges (list) – List of the pairs of candidates describing the edges in the majority graph. If \((c,d)\) is in the list of edges, then there is an edge from \(c\) to \(d\).
cmap (dict[int: str], optional) – Dictionary mapping candidates to candidate names (strings). If not provided, each candidate name is mapped to itself.

Example:

The following code creates a majority graph in which 0 is majority preferred to 1, 1 is majority preferred to 2, and 2 is majority preferred to 0:

mg = MajorityGraph([0, 1, 2], [(0,1), (1,2), (2,0)])

Warning

Currently, there is no check that the edge relation is asymmetric. It is assumed that the user provides an appropriate set of edges.

candidates¶: The list of candidates.

cindex_to_cand¶: A dictionary mapping each candidate to its index in the list of candidates and vice versa.

condorcet_loser(curr_cands=None)[source]¶

Returns the Condorcet loser in the profile restricted to curr_cands if one exists, otherwise returns None.

A candidate \(c\) is a Condorcet loser if every other candidate is majority preferred to \(c\).

condorcet_winner(curr_cands=None)[source]¶

Returns the Condorcet winner in the profile restricted to curr_cands if one exists, otherwise returns None.

The Condorcet winner is the candidate that is majority preferred to every other candidate.

copeland_scores(curr_cands=None, scores=(1, 0, -1))[source]¶

The Copeland scores in the profile restricted to the candidates in curr_cands.

The Copeland score for candidate \(c\) is calculated as follows: \(c\) receives scores[0] points for every candidate that \(c\) is majority preferred to, scores[1] points for every candidate that is tied with \(c\), and scores[2] points for every candidate that is majority preferred to \(c\). The default scores is (1, 0, -1).

Parameters:

curr_cands (list[int], optional) – restrict attention to candidates in this list. Defaults to all candidates in the profile if not provided.
scores (tuple[int], optional) – the scores used to calculate the Copeland score of a candidate \(c\): scores[0] is for the candidates that \(c\) is majority preferred to; scores[1] is for the candidates tied with \(c\); and scores[2] is for the candidates majority preferred to \(c\). The default value is scores = (1, 0, -1)

Returns:

a dictionary associating each candidate in curr_cands with its Copeland score.

cycles(curr_cands=None)[source]¶

Returns True if the margin graph has a cycle.

This uses the networkx method networkx.find_cycle to find the cycles in self.mg.

Example:

from pref_voting.weighted_majority_graphs import MajorityGraph
mg = MajorityGraph([0,1,2], [(0,1), (1,2), (0,2)])
print(f"The cycles in the majority graph are {mg.cycles()}")
mg = MajorityGraph([0,1,2], [(0,1), (1,2), (2,0)])
print(f"The cycles in the majority graph are {mg.cycles()}")
mg = MajorityGraph([0,1,2,3], [(0,1), (3,0), (1,2), (3,1), (2,0), (3,2)])
print(f"The cycles in the majority graph are {mg.cycles()}")

The cycles in the majority graph are []
The cycles in the majority graph are [[0, 1, 2]]
The cycles in the majority graph are [[0, 1, 2]]

description()[source]¶: Returns a string describing the Majority Graph.

display(cmap=None, curr_cands=None)[source]¶

Display a majority graph (restricted to curr_cands) using networkx.draw.

Parameters:

cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)
curr_cands (list[int], optional) – list of candidates

Return type:

None

Example:

from pref_voting.weighted_majority_graphs import MajorityGraph
mg = MajorityGraph([0,1,2], [(0,1), (1,2), (2,0)])
mg.display()

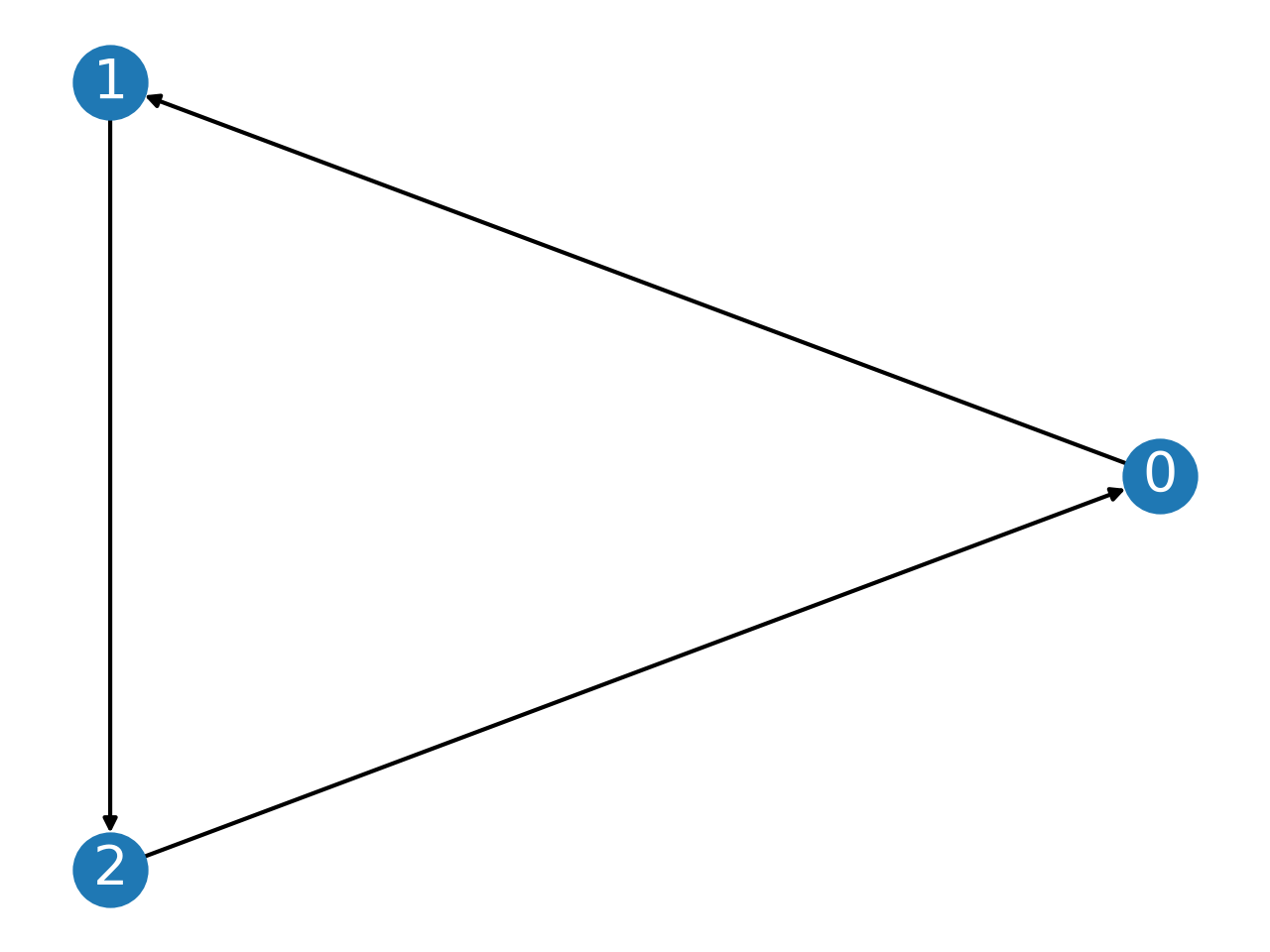
display_cycles(cmap=None)[source]¶

Display the cycles in the margin graph.

Parameters:: cmap (dict, optional) – The cmap used to map candidates to candidate names

dominates(cand, curr_cands=None)[source]¶: Returns the list of candidates that cand is majority preferred to in the majority graph restricted to curr_cands.

dominators(cand, curr_cands=None)[source]¶: Returns the list of candidates that are majority preferred to cand in the majority graph restricted to curr_cands.

property edges¶: Returns a list of the edges in the majority graph.

classmethod from_profile(profile, cmap=None)[source]¶

Generates a majority graph from a Profile.

Parameters:

profile (Profile) – the profile
cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)

Return type:

str

Example:

from pref_voting.profiles import Profile
from pref_voting.weighted_majority_graphs import MajorityGraph
prof = Profile([[0,1,2], [1,2,0], [2,0,1]])
mg = MajorityGraph.from_profile(prof)
print(mg.edges)

# it is better to use the Profile method
mg = prof.majority_graph()
print(mg.edges)

[(0, 1), (1, 2), (2, 0)]
[(0, 1), (1, 2), (2, 0)]

has_cycle(curr_cands=None)[source]¶: Returns True if there is a cycle in the majority graph.

is_tied(c1, c2)[source]¶: Returns true if there is no edge from c1 to c2 or from c2 to c1.

property is_tournament¶: Returns True if the majority graph is a tournament (there is an edge between any two distinct nodes).

maj_matrix¶: A matrix of Boolean values representing the majority graph.

majority_prefers(c1, c2)[source]¶: Returns true if there is an edge from c1 to c2.

mg¶: A networkx DiGraph object representing the majority graph.

num_cands¶: The number of candidates.

remove_candidates(cands_to_ignore)[source]¶

Remove all candidates from cands_to_ignore from the Majority Graph.

Parameters:: cands_to_ignore (list[int]) – list of candidates to remove from the profile
Returns:: a majority graph with candidates from cands_to_ignore removed and a dictionary mapping the candidates from the new profile to the original candidate names.
Example:

from pref_voting.weighted_majority_graphs import MajorityGraph
mg = MajorityGraph([0, 1, 2], [(0, 1), (1, 2), (2, 0)])
print(f"Candidates: {mg.candidates}")
print(f"Edges: {mg.edges}")
mg_new = mg.remove_candidates([1])
print(f"Candidates: {mg_new.candidates}")
print(f"Edges: {mg_new.edges}")

Candidates: [0, 1, 2]
Edges: [(0, 1), (1, 2), (2, 0)]
Candidates: [0, 2]
Edges: [(2, 0)]

to_latex(cmap=None, new_cand=None)[source]¶

Outputs TikZ code for displaying the majority graph.

Parameters:

cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)
new_cand (int) – the candidate that is displayed on the far right, only used for displaying 5 candidates.

Return type:

str

Warning

This works best for 3, 4 or 5 candidates. It will produce the code for more than 5 outputs, but the positioning of the nodes may need to be modified.

Example:

from pref_voting.weighted_majority_graphs import MajorityGraph
mg = MajorityGraph([0,1,2], [(0,1), (1,2), (2,0)])
print(mg.to_latex())
print(mg.to_latex(cmap = {0:"a", 1:"b", 2:"c"}))

\begin{tikzpicture}
\node[circle,draw,minimum width=0.25in] at (0,0) (a) {$0$}; 
\node[circle,draw,minimum width=0.25in] at (3,0) (c) {$2$}; 
\node[circle,draw,minimum width=0.25in] at (1.5,1.5) (b) {$1$};
\path[->,draw,thick] (a) to  (b);
\path[->,draw,thick] (b) to  (c);
\path[->,draw,thick] (c) to  (a);
\end{tikzpicture}

\begin{tikzpicture}
\node[circle,draw,minimum width=0.25in] at (0,0) (a) {$a$}; 
\node[circle,draw,minimum width=0.25in] at (3,0) (c) {$c$}; 
\node[circle,draw,minimum width=0.25in] at (1.5,1.5) (b) {$b$};
\path[->,draw,thick] (a) to  (b);
\path[->,draw,thick] (b) to  (c);
\path[->,draw,thick] (c) to  (a);
\end{tikzpicture}

to_networkx()[source]¶: Return a networkx weighted DiGraph representing the margin graph.

weak_condorcet_winner(curr_cands=None)[source]¶

Returns a list of the weak Condorcet winners in the profile restricted to curr_cands (which may be empty).

A candidate \(c\) is a weak Condorcet winner if there is no other candidate that is majority preferred to \(c\).

Note

While the Condorcet winner is unique if it exists, there may be multiple weak Condorcet winners.

MarginGraph Class¶

class pref_voting.weighted_majority_graphs.MarginGraph(candidates, w_edges, cmap=None)[source]¶

Bases: MajorityGraph

A margin graph is a weighted asymmetric directed graph. The nodes are the candidates and an edge from candidate \(c\) to \(d\) with weight \(w\) means that \(c\) is majority preferred to \(d\) by a margin of \(w\).

Parameters:

candidates (list[int] or list[str]) – List of the candidates. To be used as nodes in the majority graph.
w_edges (list) – List of the pairs of candidates describing the edges in the majority graph. If \((c,d,w)\) is in the list of edges, then there is an edge from \(c\) to \(d\) with weight \(w\).
cmap (dict[int: str], optional) – Dictionary mapping candidates to candidate names (strings). If not provided, each candidate name is mapped to itself.

Example:

The following code creates a margin graph in which 0 is majority preferred to 1 by a margin of 1, 1 is majority preferred to 2 by a margin of 3, and 2 is majority preferred to 0 by a margin of 5:

mg = MarginGraph([0, 1, 2], [(0,1,1), (1,2,3), (2,0,5)])

Warning

Currently, there is no check that the edge relation is asymmetric or that weights of edges are positive. It is assumed that the user provides an appropriate set of edges with weights.

description()[source]¶: Returns a string describing the Margin Graph.

display(curr_cands=None, cmap=None)[source]¶

Display a margin graph (restricted to curr_cands) using networkx.draw.

Parameters:

cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)
curr_cands (list[int], optional) – list of candidates

Return type:

None

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
mg = MarginGraph([0,1,2], [(0,1,3), (1,2,1), (2,0,5)])
mg.display()

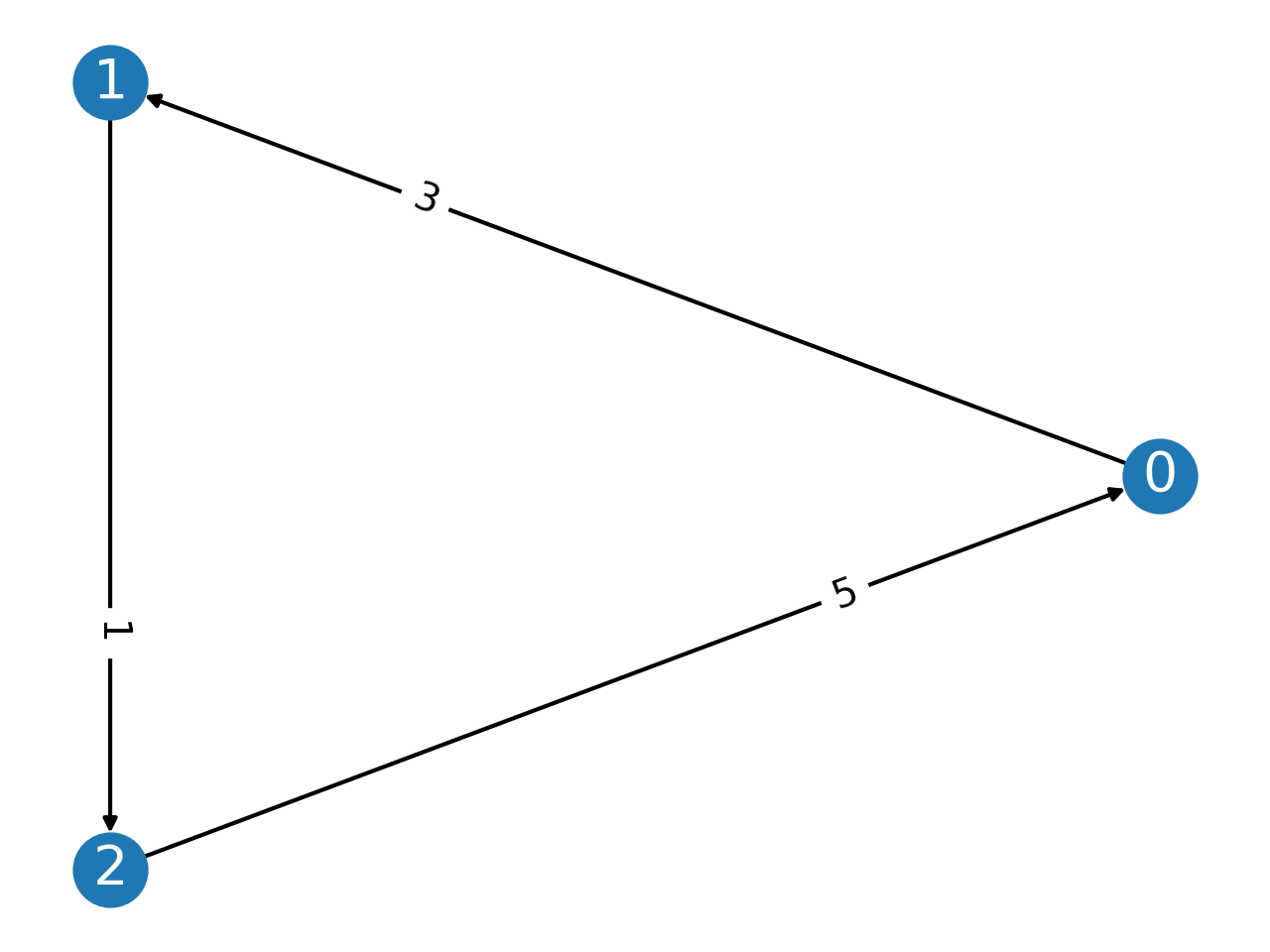
display_cycles(cmap=None)[source]¶

Display the cycles in the margin graph.

Parameters:: cmap (dict, optional) – The cmap used to map candidates to candidate names.

display_with_defeat(defeat, curr_cands=None, show_undefeated=True, cmap=None)[source]¶

Display the margin graph with any edges that are defeat edges highlighted in blue.

Parameters:

defeat (networkx.DiGraph) – The defeat relation represented as a networkx object.
curr_cands (List[int], optional) – If set, then use the defeat relation for the profile restricted to the candidates in curr_cands
show_undefeated (bool, optional) – If true, color the undefeated candidates blue and the other candidates red.
cmap (dict, optional) – The cmap used to map candidates to candidate names

property edges¶: Returns a list of the weighted edges in the margin graph.

classmethod from_profile(profile, cmap=None)[source]¶

Generates a majority graph from a Profile.

Parameters:

profile (Profile) – the profile
cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)

Return type:

str

Example:

from pref_voting.profiles import Profile
from pref_voting.weighted_majority_graphs import MarginGraph
prof = Profile([[0,1,2], [1,2,0], [2,0,1]], [2, 1, 2])
mg = MarginGraph.from_profile(prof)
print(mg.edges)
print(mg.margin_matrix)

# it is better to use the Profile method
mg = prof.margin_graph()
print(mg.edges)
print(mg.margin_matrix)

[(0, 1, 3), (1, 2, 1), (2, 0, 1)]
[[0, 3, -1], [-3, 0, 1], [1, -1, 0]]
[(0, 1, 3), (1, 2, 1), (2, 0, 1)]
[[0, 3, -1], [-3, 0, 1], [1, -1, 0]]

is_tied(c1, c2)[source]¶: Returns True if the margin c1 over c2 is zero.

is_uniquely_weighted()[source]¶: Returns True if all the margins between distinct candidates are unique and there is no 0 margin between distinct candidates.

majority_prefers(c1, c2)[source]¶: Returns True if the margin of c1 over c2 is positive.

margin(c1, c2)[source]¶: Returns the margin of c1 over c2.

margin_matrix¶: The margin matrix, where the \((i, j)\)-entry is the number of voters who rank candidate with index \(i\) above the candidate with index \(j\) minus the number of voters who rank candidate with index \(j\) above the candidate with index \(i\).

minimal_profile()[source]¶: Use an integer linear program to find a minimal profile generating the margin graph.

normalize_ordered_weights()[source]¶: Returns a MarginGraph with the same order of the edges, except that the weights are 2, 4, 6,…

Important

This function returns a margin graph that has the same ordering of the edges, but the edges may have different weights. Qualitative margin graph invariant voting methods will identify the same winning sets for both graphs.

remove_candidates(cands_to_ignore)[source]¶

Remove all candidates from cands_to_ignore from the Majority Graph.

Parameters:: cands_to_ignore (list[int]) – list of candidates to remove from the profile
Returns:: a majority graph with candidates from cands_to_ignore removed and a dictionary mapping the candidates from the new profile to the original candidate names.
Example:

from pref_voting.weighted_majority_graphs import MarginGraph
mg = MarginGraph([0, 1, 2], [(0, 1, 11), (1, 2, 13), (2, 0, 5)])
print(f"Candidates: {mg.candidates}")
print(f"Edges: {mg.edges}")
mg_new = mg.remove_candidates([1])
print(f"Candidates: {mg_new.candidates}")
print(f"Edges: {mg_new.edges}")

Candidates: [0, 1, 2]
Edges: [(0, 1, 11), (1, 2, 13), (2, 0, 5)]
Candidates: [0, 2]
Edges: [(2, 0, 5)]

strength_matrix(curr_cands=None, strength_function=None)[source]¶: Return the strength matrix of the profile. The strength matrix is a matrix where the entry in row \(i\) and column \(j\) is the number of voters that rank the candidate with index \(i\) over the candidate with index \(j\). If curr_cands is provided, then the strength matrix is restricted to the candidates in curr_cands. If strength_function is provided, then the strength matrix is computed using the strength function.

to_networkx()[source]¶: Return a networkx weighted DiGraph representing the margin graph.

SupportGraph Class¶

class pref_voting.weighted_majority_graphs.SupportGraph(candidates, w_edges, cmap=None)[source]¶

Bases: MajorityGraph

A support graph is a weighted asymmetric directed graph. The nodes are the candidates and an edge from candidate \(c\) to \(d\) with weight \(w\) means that the support of \(c\) over \(d\) is \(w\).

Parameters:

candidates (list[int] or list[str]) – List of the candidates. To be used as nodes in the majority graph.
w_edges (list) – List representing the edges in the majority graph with supports. If \((c,d,(n,m))\) is in the list of edges, then there is an edge from \(c\) to \(d\), the support for \(c\) over \(d\) is \(n\), and the support for \(d\) over \(c\) is \(m\).
cmap (dict[int: str], optional) – Dictionary mapping candidates to candidate names (strings). If not provided, each candidate name is mapped to itself.

Example:

The following code creates a support graph in which:

0 is majority preferred to 1, the number of voters who rank 0 over 1 is 4, and the number of voters who rank 1 over 0 is 3;
1 is majority preferred to 2, the number of voters who rank 1 over 2 is 5, and the number of voters who rank 2 over 1 is 2; and
2 is majority preferred to 0, the number of voters who rank 2 over 0 is 6, and the number of voters who rank 0 over 2 is 1.

sg = SupportGraph([0, 1, 2], [(0, 1, (4, 3)), (1, 2, (5, 2)), (2, 0, (6, 1))])

Warning

Currently, there is no check to that the edge relation is asymmetric. It is assumed that the user provides an appropriate set of edges with weights.

display(curr_cands=None, cmap=None)[source]¶

Display a support graph (restricted to curr_cands) using networkx.draw.

Parameters:

cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)
curr_cands (list[int], optional) – list of candidates

Return type:

None

property edges¶: Returns a list of the weighted edges in the margin graph.

classmethod from_profile(profile, cmap=None)[source]¶

Generates a support graph from a Profile.

Parameters:

profile (Profile) – the profile
cmap (dict[int,str], optional) – the candidate map to use (overrides the cmap associated with this majority graph)

Return type:

str

Example:

from pref_voting.profiles import Profile
from pref_voting.weighted_majority_graphs import SupportGraph
prof = Profile([[0,1,2], [1,2,0], [2,0,1]], [2, 1, 2])
sg = SupportGraph.from_profile(prof)
print(sg.edges)
print(sg.s_matrix)

# it is better to use the Profile method
sg = prof.support_graph()
print(sg.edges)
print(sg.s_matrix)

[(0, 1, (4, 1)), (1, 2, (3, 2)), (2, 0, (3, 2))]
[[0, 4, 2], [1, 0, 3], [3, 2, 0]]
[(0, 1, (4, 1)), (1, 2, (3, 2)), (2, 0, (3, 2))]
[[0, 4, 2], [1, 0, 3], [3, 2, 0]]

is_tied(c1, c2)[source]¶: Returns True if c1 is tied with c2.

majority_prefers(c1, c2)[source]¶: Returns True if c1 is majority preferred to c2.

margin(c1, c2)[source]¶: Returns the margin of c1 over c2.

remove_candidates(cands_to_ignore)[source]¶

Remove all candidates from cands_to_ignore from the Majority Graph.

Parameters:: cands_to_ignore (list[int]) – list of candidates to remove from the profile
Returns:: a majority graph with candidates from cands_to_ignore removed and a dictionary mapping the candidates from the new profile to the original candidate names.
Example:

from pref_voting.weighted_majority_graphs import SupportGraph
sg = SupportGraph([0, 1, 2], [(0, 1, (11, 1)), (1, 2, (5, 13)), (2, 0, (5, 10))])
print(f"Candidates: {sg.candidates}")
print(f"Edges: {sg.edges}")
sg_new = sg.remove_candidates([1])
print(f"Candidates: {sg_new.candidates}")
print(f"Edges: {sg_new.edges}")

Candidates: [0, 1, 2]
Edges: [(0, 1, (11, 1)), (0, 2, (10, 5)), (2, 1, (13, 5))]
Candidates: [0, 2]
Edges: [(0, 2, (10, 5))]

s_matrix¶: The support matrix, where the \((i, j)\)-entry is the number of voters who rank candidate with index \(i\) above the candidate with index \(j\).

strength_matrix(curr_cands=None, strength_function=None)[source]¶: Return the strength matrix of the profile. The strength matrix is a matrix where the entry in row \(i\) and column \(j\) is the number of voters that rank the candidate with index \(i\) over the candidate with index \(j\). If curr_cands is provided, then the strength matrix is restricted to the candidates in curr_cands. If strength_function is provided, then the strength matrix is computed using the strength function.

support(c1, c2)[source]¶: Returns the support of c1 over c2.