C1 Methods¶

Suppose that \(\mathbf{P}\) is a profile. We write \(M(\mathbf{P})\) for the majority graph of \(\mathbf{P}\).

A voting method \(F\) is C1 if it satisfies the following invariance property: For all \(\mathbf{P}, \mathbf{P}'\), if \(M(\mathbf{P})= M(\mathbf{P}')\), then \(F(\mathbf{P}) = F(\mathbf{P}')\).

Condorcet¶

pref_voting.c1_methods.condorcet(edata, curr_cands=None)[source]¶

Return the Condorcet winner if one exists, otherwise return all the candidates. A Condorcet winner is a candidate \(c\) that is majority preferred to every other candidate.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a condorcet_winner method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
from pref_voting.c1_methods import condorcet

prof = Profile([[0, 1, 2], [1, 2, 0], [2, 0, 1]], [1, 1, 1])

prof.display()
print(prof.condorcet_winner())
condorcet.display(prof)
condorcet.display(prof.majority_graph())
condorcet.display(prof.margin_graph())

prof2 = Profile([[0, 1, 2], [2, 1, 0], [1, 0, 2]], [3, 1, 1])

prof2.display()
print(prof2.condorcet_winner())
condorcet.display(prof2)
condorcet.display(prof2.majority_graph())
condorcet.display(prof2.margin_graph())

+---+---+---+
| 1 | 1 | 1 |
+---+---+---+
| 0 | 1 | 2 |
| 1 | 2 | 0 |
| 2 | 0 | 1 |
+---+---+---+
None
Condorcet winners are {0, 1, 2}
Condorcet winners are {0, 1, 2}
Condorcet winners are {0, 1, 2}
+---+---+---+
| 3 | 1 | 1 |
+---+---+---+
| 0 | 2 | 1 |
| 1 | 1 | 0 |
| 2 | 0 | 2 |
+---+---+---+
0
Condorcet winner is {0}
Condorcet winner is {0}
Condorcet winner is {0}

Copeland¶

pref_voting.c1_methods.copeland(edata, curr_cands=None)[source]¶

The Copeland score for c is the number of candidates that c is majority preferred to minus the number of candidates majority preferred to c. The Copeland winners are the candidates with the maximum Copeland score in the profile restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a copeland_scores method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[1, 3, 0, 4, 2], [0, 1, 4, 2, 3], [2, 4, 0, 1, 3], [3, 0, 2, 4, 1],  [4, 3, 1, 0, 2], [2, 3, 0, 1, 4]], [1, 1, 1, 1, 1, 1])

prof.display_margin_graph()

(Source code, png, pdf)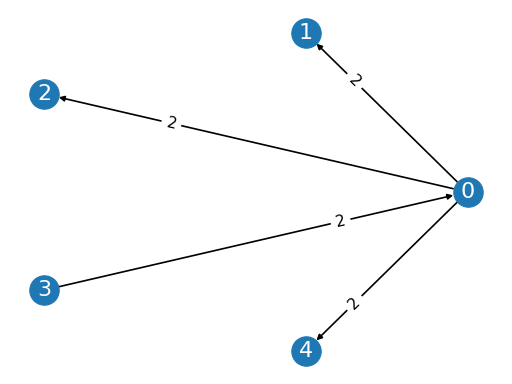

from pref_voting.c1_methods import copeland
copeland.display(prof)

Copeland winner is {0}
{0: 2.0, 1: -1.0, 2: -1.0, 3: 1.0, 4: -1.0}

Llull¶

pref_voting.c1_methods.llull(edata, curr_cands=None)[source]¶

The Llull score for a candidate \(c\) is the number of candidates that \(c\) is weakly majority preferred to. This is equivalent to calculating the Copeland scores for a candidate \(c\) with 1 point for each candidate that \(c\) is majority preferred to, 1/2 point for each candidate that \(c\) is tied with, and 0 points for each candidate that is majority preferred to \(c\). The Llull winners are the candidates with the maximum Llull score in the profile restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a copeland_scores method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[1, 3, 0, 4, 2], [0, 1, 4, 2, 3], [2, 4, 0, 1, 3], [3, 0, 2, 4, 1],  [4, 3, 1, 0, 2], [2, 3, 0, 1, 4]], [1, 1, 1, 1, 1, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.c1_methods import llull
llull.display(prof)

Llull winner is {3}
{0: 3.0, 1: 1.5, 2: 1.5, 3: 2.5, 4: 1.5}

Uncovered Set¶

Uncovered Set - Gillies¶

pref_voting.c1_methods.uc_gill(edata, curr_cands=None)[source]¶

Uncovered Set (Gillies version): Given candidates \(a\) and \(b\), say that \(a\) defeats \(b\) in the election if \(a\) is majority preferred to \(b\) and \(a\) left covers \(b\): i.e., for all \(c\), if \(c\) is majority preferred to \(a\), then \(c\) majority preferred to \(b\). The winners are the set of candidates who are undefeated in the election restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a dominators method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[2, 3, 0, 1], [0, 2, 1, 3], [3, 0, 1, 2], [1, 2, 0, 3], [1, 2, 3, 0]], [1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)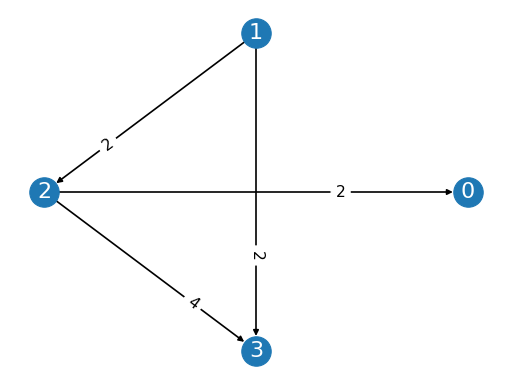

from pref_voting.c1_methods import uc_gill
uc_gill.display(prof)

Uncovered Set winners are {0, 1}

Uncovered Set Defeat (Gillies Version)¶

pref_voting.c1_methods.uc_gill_defeat(edata, curr_cands=None)[source]¶

Returns the defeat relation used to find the Uncovered Set (Gillies version) winners.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a dominators method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A networkx object in which there is an edge from \(a\) to \(b\) when \(a\) to \(b\) according to Top Cycle.

See also

pref_voting.c1_methods.uc_gill()

Example:

from pref_voting.profiles import Profile
from pref_voting.c1_methods import uc_gill_defeat

prof = Profile(
    [
        [0, 3, 1, 2],
        [3, 2, 0, 1],
        [2, 0, 3, 1],
        [3, 2, 1, 0],
        [0, 2, 3, 1],
        [3, 1, 2, 0],
        [2, 3, 0, 1]
    ],
    [1, 1, 1, 1, 3, 2, 1])

uc_gill_def = uc_gill_defeat(prof)

prof.display_margin_graph_with_defeat(uc_gill_def, show_undefeated=True)

(Source code, png, pdf)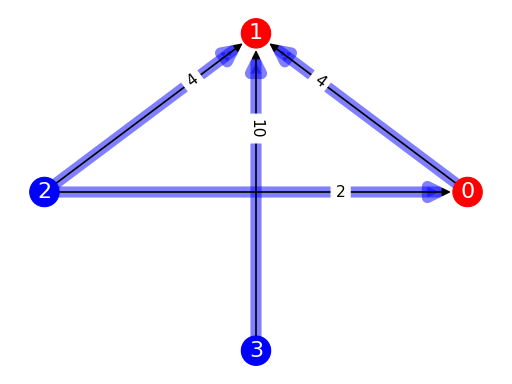

Uncovered Set - Fishburn¶

pref_voting.c1_methods.uc_fish(edata, curr_cands=None)[source]¶

Uncovered Set (Fishburn version): Given candidates \(a\) and \(b\), say that \(a\) defeats \(b\) in the election \(a\) left covers \(b\): i.e., for all \(c\), if \(c\) is majority preferred to \(a\), then \(c\) majority preferred to \(b\). The winners are the set of candidates who are undefeated in the election restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a dominators method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[2, 3, 0, 1], [0, 2, 1, 3], [3, 0, 1, 2], [1, 2, 0, 3], [1, 2, 3, 0]], [1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.c1_methods import uc_fish
uc_fish.display(prof)

Uncovered Set - Fishburn winner is {1}

Uncovered Set Defeat (Fishburn Version)¶

pref_voting.c1_methods.uc_fish_defeat(edata, curr_cands=None)[source]¶

Returns the defeat relation used to find the Uncovered Set (Fishburn version) winners.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a dominators method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A networkx object in which there is an edge from \(a\) to \(b\) when \(a\) to \(b\) according to Top Cycle.

See also

pref_voting.c1_methods.uc_fish()

Example:

from pref_voting.profiles import Profile
from pref_voting.c1_methods import uc_fish_defeat

prof = Profile(
    [
        [0, 3, 1, 2],
        [3, 2, 0, 1],
        [2, 0, 3, 1],
        [3, 2, 1, 0],
        [0, 2, 3, 1],
        [3, 1, 2, 0],
        [2, 3, 0, 1]
    ],
    [1, 1, 1, 1, 3, 2, 1])

uc_fish_def = uc_fish_defeat(prof)

prof.display_margin_graph_with_defeat(uc_fish_def, show_undefeated=True)

(Source code, png, pdf)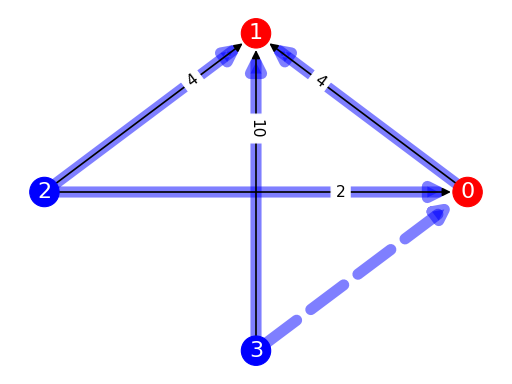

Uncovered Set - Bordes¶

pref_voting.c1_methods.uc_bordes(edata, curr_cands=None)[source]¶

Uncovered Set (Bordes version): Given candidates \(a\) and \(b\), say that \(a\) Bordes covers \(b\) if \(a\) is majority preferred to \(b\) and for all \(c\), if \(c\) is majority preferred or tied with \(a\), then \(c\) is majority preferred to or tied with \(b\). The winners are the set of candidates who are not Bordes covered in the election restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has dominators and majority_prefers methods.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[2, 3, 0, 1], [0, 2, 1, 3], [3, 0, 1, 2], [1, 2, 0, 3], [1, 2, 3, 0]], [1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.c1_methods import uc_bordes
uc_bordes.display(prof)

Uncovered Set - Bordes winners are {1, 2}

Uncovered Set - McKelvey¶

pref_voting.c1_methods.uc_mckelvey(edata, curr_cands=None)[source]¶

Uncovered Set (McKelvey version): Given candidates \(a\) and \(b\), say that \(a\) McKelvey covers \(b\) if a Gillies covers \(b\) and \(a\) Bordes covers \(b\). The winners are the set of candidates who are not McKelvey covered in the election restricted to curr_cands.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has dominators and majority_prefers methods.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[2, 3, 0, 1], [0, 2, 1, 3], [3, 0, 1, 2], [1, 2, 0, 3], [1, 2, 3, 0]], [1, 1, 1, 2, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.c1_methods import uc_mckelvey
uc_bordes.display(prof)

Uncovered Set - McKelvey winners are {0, 1, 2}

Top Cycle¶

pref_voting.c1_methods.top_cycle(edata, curr_cands=None)[source]¶

The smallest set of candidates such that every candidate inside the set is majority preferred to every candidate outside the set.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a majority_prefers method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

See also

Also known as getcha and smith_set.

Related function includes pref_voting.c1_methods.gocha()

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[1, 2, 0, 3], [1, 3, 0, 2], [3, 1, 0, 2], [0, 3, 1, 2]], [1, 1, 1, 1])

prof.display_margin_graph()

(Source code, png, pdf)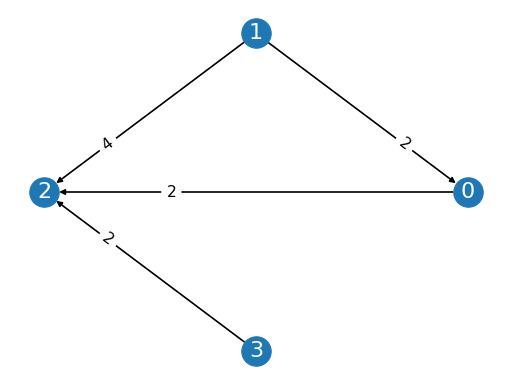

from pref_voting.c1_methods import top_cycle, getcha, smith_set
top_cycle.display(prof)
getcha.display(prof)
smith_set.display(prof)

Top Cycle winners are {0, 1, 3}
GETCHA winners are {0, 1, 3}
Smith Set winners are {0, 1, 3}

Top Cycle Defeat¶

pref_voting.c1_methods.top_cycle_defeat(edata, curr_cands=None)[source]¶

Return the defeat relation associated with the Top Cycle voting method.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a majority_prefers method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A networkx object in which there is an edge from \(a\) to \(b\) when \(a\) to \(b\) according to Top Cycle.

See also

pref_voting.c1_methods.top_cycle()

Example:

from pref_voting.profiles import Profile
from pref_voting.c1_methods import top_cycle_defeat

prof = Profile(
    [
        [0, 1, 2, 3], 
        [1, 2, 0, 3], 
        [2, 0, 1, 3]
    ], 
    [1, 1, 1])

tc_defeat = top_cycle_defeat(prof)

prof.display_margin_graph_with_defeat(tc_defeat, show_undefeated=True)

(Source code, png, pdf)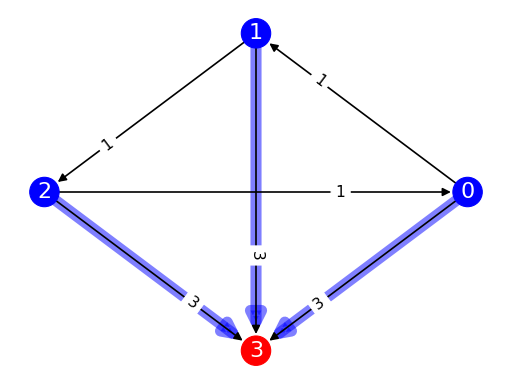

GOCHA¶

pref_voting.c1_methods.gocha(edata, curr_cands=None)[source]¶

The GOCHA set (also known as the Schwartz set) is the set of all candidates x such that if y can reach x in the transitive closer of the majority relation, then x can reach y in the transitive closer of the majority relation.

Parameters:

edata (Profile, ProfileWithTies, MajorityGraph, MarginGraph) – Any election data that has a majority_prefers method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

See also

Also known as schwartz_set.

Related function includes pref_voting.c1_methods.top_cycle()

Example:

from pref_voting.profiles import Profile
        
prof = Profile([[1, 2, 0, 3], [1, 3, 0, 2], [3, 1, 0, 2], [0, 3, 1, 2]], [1, 1, 1, 1])

prof.display_margin_graph()

(Source code, png, pdf)

from pref_voting.c1_methods import top_cycle, gocha, schwartz_set

gocha.display(prof)
schwartz_set.display(prof)

GOCHA winners are {1, 3}
Schwartz Set winners are {1, 3}

Banks¶

pref_voting.c1_methods.banks(edata, curr_cands=None)[source]¶

Say that a chain in majority graph is a subset of candidates that is linearly ordered by the majority relation. Then a candidate \(a\) if \(a\) is the maximum element with respect to the majority relation of some maximal chain in the majority graph.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 2), (0, 3, 6), (1, 0, 8), (2, 3, 4), (2, 1, 10), (3, 1, 12)])

mg.display()

(Source code, png, pdf)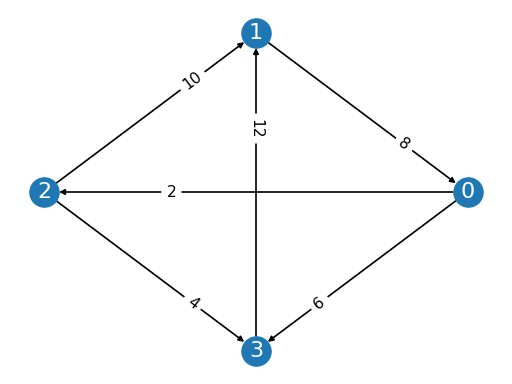

from pref_voting.c1_methods import banks

banks.display(prof)

Banks winners are {0, 1, 2}

Banks with Explanation¶

pref_voting.c1_methods.banks_with_explanation(edata, curr_cands=None)[source]¶

Return the Banks winners and the list of maximal chains in the majority graph.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

A list of lists of candidates each representing a maximal chain in the majority graph

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 2), (0, 3, 6), (1, 0, 8), (2, 3, 4), (2, 1, 10), (3, 1, 12)])

mg.display()

(Source code, png, pdf)

from pref_voting.c1_methods import banks_with_explanation

bws, maximal_chains = banks_with_explanation(mg)

print(f"Winning set: {bws}")
for c in maximal_chains:
    print(f"Maximal chain: {c}")

Winning set: [0, 1, 2]
Maximal chain: (1, 0)
Maximal chain: (0, 2, 3)
Maximal chain: (2, 3, 1)

Slater¶

pref_voting.c1_methods.slater(edata, curr_cands=None)[source]¶

A Slater ranking is a linear order \(R\) of the candidates that minimizes the number of edges in the majority graph we have to turn around before we obtain \(R\). A candidate is a Slater winner if the candidate is the top element of some Slater ranking.

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A sorted list of candidates

Example:

from pref_voting.weighted_majority_graphs import MarginGraph

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 2), (0, 3, 6), (1, 0, 8), (2, 3, 4), (2, 1, 10), (3, 1, 12)])

mg.display()

(Source code, png, pdf)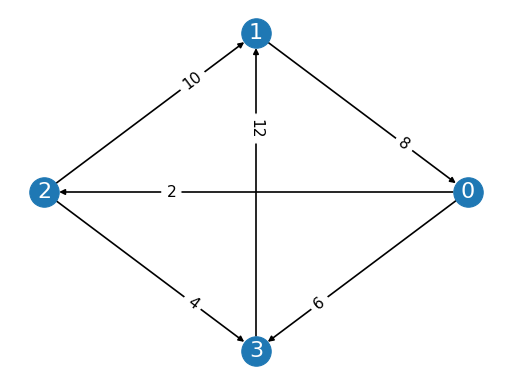

from pref_voting.c1_methods import slater

slater.display(prof)

Slater winner is {0}

Slater Rankings¶

pref_voting.c1_methods.slater_rankings(edata, curr_cands=None)[source]¶

A Slater ranking is a linear order \(R\) of the candidates that minimizes the number of edges in the majority graph we have to turn around before we obtain \(R\).

Parameters:

edata (Profile, ProfileWithTies, MarginGraph) – Any election data that has a margin method.
curr_cands (List[int], optional) – If set, then find the winners for the profile restricted to the candidates in curr_cands

Returns:

A list of Slater rankings.

dist: The minimum distance of the Slater rankings.

Return type:

rankings

Example:

from pref_voting.weighted_majority_graphs import MarginGraph
from pref_voting.c1_methods import slater_rankings

mg = MarginGraph([0, 1, 2, 3], [(0, 2, 2), (0, 3, 6), (1, 0, 8), (2, 3, 4), (2, 1, 10), (3, 1, 12)])

srs, d = slater_rankings(mg)
print(f"minimum distance: {d}")
for sr in srs:
    print(f"ranking: {sr}")

minimum distance: 1
ranking: (0, 2, 3, 1)